Formula
![]()
Variables
![]() all bearings of a GPS track
all bearings of a GPS track
![]() average bearing of a GPS track
average bearing of a GPS track
Explanation
To determine the average bearing of a GPS track u: 1
1. Get the bearings ![]() of all coordinates
of all coordinates
On the page “Bearing of 2 GPS coordinates” I explain how you can determine the bearings.
2. Convert the bearings ![]() to unit vectors
to unit vectors ![]()
![]()
3. Take the average of the unit vector ![]()
![]()
4. convert the average unit vector back to a bearing ![]()
To convert the average unit vector ![]() back to a bearing
back to a bearing ![]() you can use atan2.
you can use atan2.
![]()
Examples
Mathmatical example
![]()
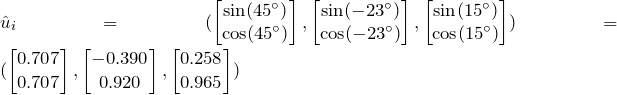
![]()
![]()
